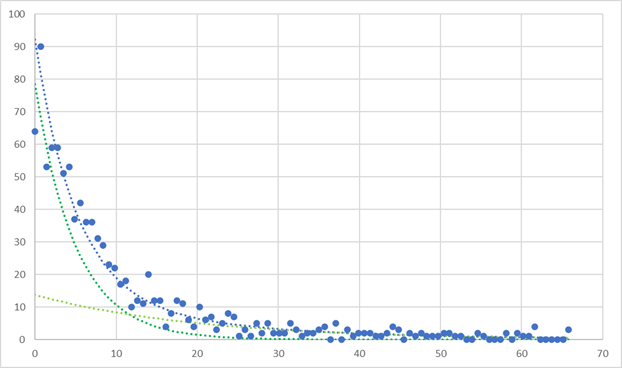
・二つの指数関数の和
二つの指数関数の和の確率密度は,
\(\Large \displaystyle P(x) = A_0 \left[ p \cdot exp (-k_1 \ x) + (1-p) \cdot exp (-k_2 \ x) \right] \)
です.この場合の比例係数,A0,は,
\(\Large \displaystyle \int_0^{\infty} A_0 \left[ p \cdot exp (-k_1 \ x) + (1-p) \cdot exp (-k_2 \ x) \right] dx \)
となります.それぞれ独立に積分できるので,
\(\Large \displaystyle = \int_0^{\infty} A_0 p \cdot exp (-k_1 \ x) dx + \int_0^{\infty} A_0 (1-p) \cdot exp (-k_2 \ x) dx \)
\(\Large \displaystyle = - \frac{A_0 p}{k_1} [0-1] - \frac{A_0 (1-p)}{k_2} [0-1]\)
\(\Large \displaystyle = A_0 \left[ \frac{p}{k_1} + \frac{1-p}{k_2} \right] \)
\(\Large \displaystyle = A_0 \left[ \frac{p k_2 +(1-p) k_1}{k_1 k_2} \right] = 1\)
となるので,
\(\Large \displaystyle A_0 = \frac{k_1 k_2}{p k_2 +(1-p) k_1} \)
となります,したがって確率密度は,
\(\Large \displaystyle P(x) = \frac{k_1 k_2}{p k_2 +(1-p) k_1} \left[ p \cdot exp (-k_1 \ x) + (1-p) \cdot exp (-k_2 \ x) \right] \)
となります.
解法:
bin(d)ごとに集計します.
その総和は推定したデータ数,N,となりますので,
\(\Large \displaystyle N = N_1 + N_2 = Np + N(1-p) = C_1 \cdot \sum_{i=0}^\infty \left[ exp (-k_1 \ d \ i) \right] + C_2 \cdot \sum_{i=0}^\infty \left[ exp (-k_2 \ d \ i) \right]\)
\(\Large \displaystyle N_1 = Np = C_1 \cdot \sum_{i=0}^\infty \left[ exp (-k_1 \ d \ i) \right] \)
\(\Large \displaystyle N_2 = Np = C_2 \cdot \sum_{i=0}^\infty \left[ exp (-k_2 \ d \ i) \right] \)
と別々に計算すればいいので.それぞれに計算すると,
\(\Large \displaystyle N_1 = Np = C_1 \frac{1}{1 - exp (-k_1 \ d )} \Rightarrow C_1 = Np [1 - exp (-k_1 \ d )] \)
\(\Large \displaystyle N_2 = Np = C_2 \frac{1}{1 - exp (-k_2 \ d )} \Rightarrow C_2 = N(1-p) [1 - exp (-k_2 \ d )] \)
となるので,C1+C2の高さを基準とした関数となるわけです.
・実際の計算
実際に,ランダム関数から指数分布を二つ作成して(詳細はここ),k,dを色々変えて計算させると,
k1=0.2, k2=0.05,p=0.6, d=0.7, N=1000, -> 94.143

k1=0.2, k2=0.05,p=0.6, d=1, N=1000, -> 128.27
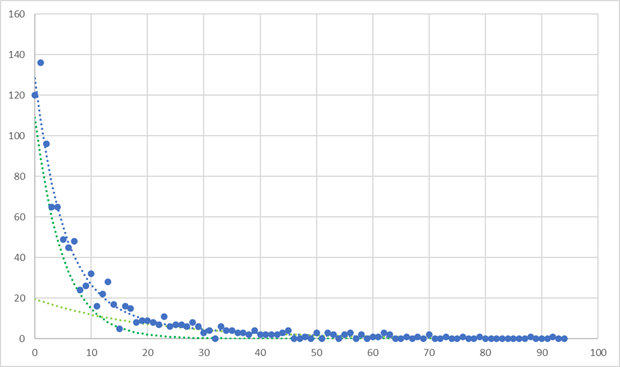
k1=0.3, k2=0.05,p=0.6, d=1, N=1000, -> 175.02
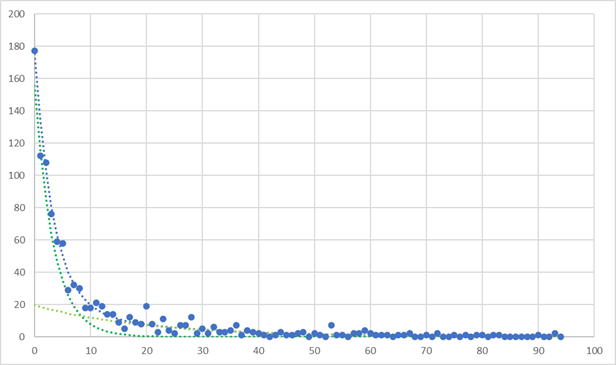
ときれいにフィットできました.
次は,逐次反応,の場合です.